| En el capítulo de dinámica hemos estudiado las colisiones
unidimensionales elásticas e inelásticas tanto desde el punto de vista de un
observador situado en el Sistema de Referencia del Laboratorio como del Sistema de
Referencia del Centro de Masa. A continuación, procedimos con el estudio de las colisiones
bidimensionales. En ambos, hemos aplicado el principio
de conservación del momento lineal a un sistema aislado de dos partículas
interactuantes, y a continuación hemos efectuado el balance energético de la colisión.
Consideremos un sistema aislado de dos partículas interactuantes.

Comprobaremos la conservación del momento lineal y del momento angular en una
experiencia simulada de colisión entre dos dicos, y efectuaremos el balance energético
de dicha colisión.
- Tenemos un sistema aislado de dos partículas interactuantes. El principio de
conservación del momento lineal se escribe
- A lo largo del eje horizontal X
m1u1·senq1+m2u2·senq2=m1v1·senf1+m2v2·senf2
- A lo largo del vertical Y
-m1u1·cosq1+m2u2·cosq2=m1v1·cosf1-m2v2·cosf2
- Constancia del momento angular de cada uno de los discos. El momento angular respecto de
O antes y después del choque es el mismo
El momento angular de cada uno de los discos se mantiene constante. Ya que las fuerzas
que ejerce un disco sobre el otro actúan en el punto de contacto P. El momento de dichas
fuerzas respecto de P es cero. De la relación
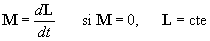
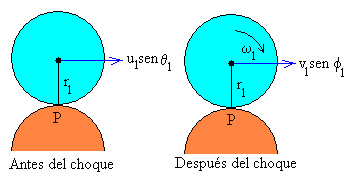
m1·r1·u1senq1=m1·r1·v1senf1+I1w1

-m2·r2·u2senq2=-m2·r2·v2senf2+I2w2
- De la definición de coeficiente
de restitución
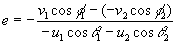
e(u1 cosq1+u2cosq2)= v1cosf1+v2cosf2
Considremos el caso de que no hay deslizamiento de un disco respecto del otro en el
punto de contacto P. Las velocidades de los dos discos en el punto de contacto P serán
iguales. Véase la figura anterior
v1senf1-r1
w 1=v2senf2+r2
w2
Sabiendo que el momento de inercia de los discos es I=mr2/2,
obtenemos la relación
3v1senf1-2·u1senq1= 3v2senf2-2·u2senq2
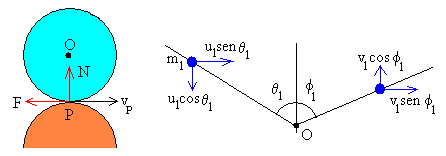
La fuerza N actuando durante el pequeño intervalo de tiempo Dt
en el que el disco y la pared están en contacto modifica la componente normal del momento
lineal del disco. De modo análogo el
impulso de la fuerza F modifica la componente paralela al plano del momento
lineal del disco. La fuerza de rozamiento F es de sentido contrario a la velocidad
del disco en el punto de contacto P, vP

De la relación ente ambas fuerzas F=m ·N, obtenemos
m ·(v1cosf1+
u1cosq1)= -v1senf1+ u1senq1

Las fuerzas en el punto de contacto P son iguales y de sentido contrario
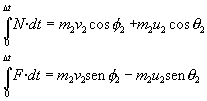
De la relación ente ambas fuerzas F=m ·N, obtenemos
m ·(v2cos f2+
u2cosq2)= v2senf2- u2senq2
Resolviendo estas ecuaciones cuando el segundo disco está en reposo, se obtienen las
velocidades después del choque v1 y v2, las
velocidades angulares de rotación w1 y w2, y los ángulos de desviación de las
partículas respecto de la dirección de la velocidad de la partícula incidente.
Consultar el artículo
Doménech A, Doménech M.T. Analysis of two-disc collisions. Eur. J. Phys. 14
(1993) 177-183.
En la deducción de las ecuaciones del choque se ha supuesto:
- Que las fuerzas normales dependen de las propiedades elásticas de los cuerpos, mientras
que las fuerzas tangenciales dependen del rozamiento entre los discos, las cuales dependen
del estado de las superficies en contacto.
- Que las fuerzas tangenciales y normales son independientes
- Que los coeficientes de restitución y de rozamiento son constantes y solamente dependen
de la naturaleza de los materiales con los que están hechos los discos.
En este applet se muestran los resultados obtenidos a partir de las ecuaciones que se
deducen en el artículo citado al comienzo de esta página y de los datos de la tabla.
Sin embargo, el objetivo de esta página es el de comprobar con un ejemplo la
conservación del momento lineal y del momento angular en un sistema aislado de dos
partículas interactuantes.
| Materiales |
Coef. restitución e |
Coef. de rozamiento m |
| Acero-acero |
0.94 |
0.10 |
| Aluminio-aluminio |
0.61 |
0.12 |
| Latón-latón |
0.57 |
0.11 |
| Acero-latón |
0.65 |
0.10 |
| Aluminio-latón |
0.55 |
0.10 |
| Acero-aluminio |
0.62 |
0.09 |
Fuente: Doménech A, Doménech M.T. Colisiones inelásticas de esferas. Revista
Española de Física 4, 3 (1990) 52-56.
Introducimos los siguientes datos relativos a los dos discos
- Cociente m2/m1 entre las masa de los discos
- Cociente r2/r1 entre los radios de los discos
- Materiales de los que están hechos los discos, véase la tabla
Parámetros iniciales antes del choque
- Velocidad inicial u1 del primer disco
- El segundo disco está inicialmente en reposo en el origen
- Parámetro de impacto, b, un número entre 0 y 2. El valor 0 es para los choques
frontales.
- La velocidad angular inicial de los discos es nula
Pulsando el botón titulado Empieza, observamos el movimiento de los discos
antes y después del choque en el Sistema de Referencia del Laboratorio
El programa interactivo calcula los parámetros después del choque: vectores velocidad
(módulo y dirección) y velocidad angular de rotación alrededor del eje de cada disco.
- Las velocidades lineales v1 y v2 de los discos
después del choque
- Los ángulos de desviación f1 y f2 de los discos respecto de la dirección del
disco incidente.
- Las velocidades angulares w1 y w2 de los discos después del choque
Con los datos introducidos y calculados por el programa, verificaremos numéricamente
el principio de conservación del momento lineal y angular.
Ejemplo 1º:
Datos relativos a los discos
- Cociente m2/m1=1 entre las masa de los discos,
- Cociente r2/r1=1 entre los radios de los discos
- Discos ambos de acero, e=0.94 y m =0.10
Antes del choque
- Velocidad inicial u1=3.5 del primer disco
- Parámetro de impacto b=1.5.
Después del choque
- Velocidad del primer disco v1=2.40, dirección f1=39.75º
- Velocidad del segundo disco v2=2.26, dirección f2=-42.88º
- Velocidad angular del primer disco w1=-0.45
(sentido de las agujas del reloj)
- Velocidad angular del segundo disco w2=-0.45
1.- Conservación del momento lineal
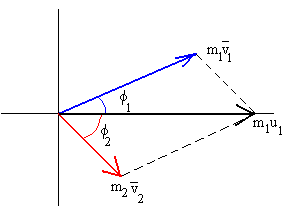 |
El momento lineal inicial del primer disco (el segundo está inicialmente
en reposo) es igual a la suma vectorial de los momentos lineales de los discos después
del choque. 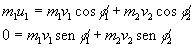
|
2.-Conservación del momento angular
- Antes del choque
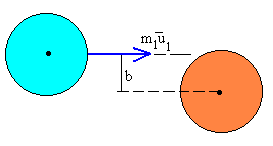 |
El momento angular inicial tal como podemos ver en la figura es
- Módulo, L=-m1u1·b (momento lineal por el brazo del
momento lineal)
- Dirección perpendicular al plano de la página
- Sentido hacia dentro (negativo)
L=-1·3.5·1.5=-5.25 |
- Después del choque
- El momento angular de traslación del primer disco (de color azul) respecto de O es
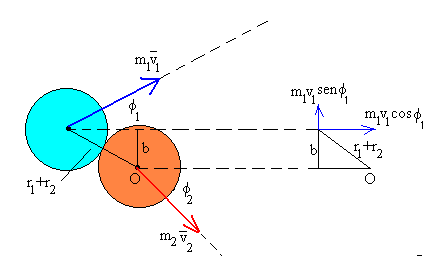 |
Descomponemos el momento lineal en su componente horizontal y vertical, y
hallamos el momento angular de cada componente. 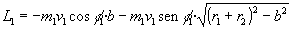
L1=-4.80 |
- Momento angular intrínseco de cada uno de los discos
 |
Como los discos están en rotación respecto a su propio eje el momento
angular total intrínseco (espín) es L2=I1w1+
I2 w2
Donde I1 e I2 son los momentos de inercia de
cada uno de los discos
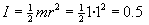
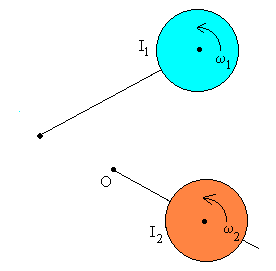
L2=-0.5·0.45-0.5·0.45=-0.45 |
El momento angular total después del choque es el momento angular de traslación más
el momento angular intrínseco (espín) de los discos
L=L1+L2
L=-4.80-0.45=-5.25
Con lo que queda comprobadas ambas leyes de conservación
3.-Balance energético
Energía inicial 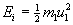
Ei=6.125
Energía final 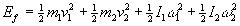
Ef=5.535
Un valor menor que la inicial.
Ejemplo 2º.
Datos relativos a los discos
- Cociente m2/m1=2 entre las masa de los discos (m2=2,
m1=1)
- Cociente r2/r1=0.5 entre los radios de los discos (r2=0.5,
r1=1)
- Discos ambos de acero, e=0.94 y m =0.10
Antes del choque
- Velocidad inicial u1=3.5 del primer disco
- Parámetro de impacto b=0.2.
Después del choque
- Velocidad del primer disco v1=1.08, dirección f1=152.71º
- Velocidad del segundo disco v2=2.24, dirección f2=-6.34º
- Velocidad angular del primer disco w1=-0.21
- Velocidad angular del segundo disco w2=-0.21
1.- Conservación del momento lineal
Eje X: 1·3.5=3.5
Eje Y: 0.0
Eje X: 1·1.08·cos152.71+2·2.24·cos(-6.34)=3.49
Eje Y: 1·1.08·sen152.71+2·2.24·sen(-6.34)=0.0004 » 0.0
El momento lineal se conserva
2.-Conservación del momento angular
L=-1·3.5·0.2=-0.7
Traslación del primer disco:
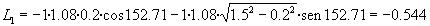
Rotación de los discos
Los momentos de inercia de los discos son

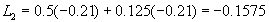
Por lo que L» L1+L2
3.-Balance energético

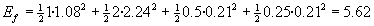
Ejemplo 3º Choques frontales
Datos relativos a los discos
- Cociente m2/m1=2 entre las masa de los discos (m2=2,
m1=1)
- Discos ambos de acero, e=0.94
Antes del choque
- Velocidad inicial u1=3.5 del primer disco
- Parámetro de impacto b=0.0.
Después del choque
- Velocidad del primer disco v1=-1.03
- Velocidad del segundo disco v2=2.26,
- Conservación del momento lineal
Eje X: 1.3.5=3.5
Eje X: -1·1.03+2·2.26=3.49
Se conserva el momento lineal
- Balance energético
Antes del choque
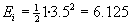
Después del choque

|