Bobine et dipôle RL

Synthèse P7

I La bobine

I-1 Définition

Une bobine est constituée d’un enroulement de fil électrique en cuivre, entouré d’une gaine ou d’un vernis isolant.

I-2 Loi d’Ohm aux bornes de la bobine

Lorsqu’une bobine d’inductance L et de résistance r est parcourue par un courant d’intensité i,

la tension u à ses bornes s’exprime par la relation :

u = L.di/dt + ri en convention récepteur

avec L exprimée en henry (H), u en volt (V), r en ohm (Ω) et i en ampère (A). L’intensité du courant parcourant une bobine est une grandeur continue.

I-3 Energie emmagasinée par la bobine

Une bobine peut acquérir de l’énergie qu’elle restitue lors de l’ouverture de l’interrupteur présent dans le circuit où elle se trouve. L’énergie E_bob s’exprime en fonction de l’intensité i qui la traverse et de l’inductance L :

E_bob = ½ Li² avec E_bob en joules (J) , L en henry (H) et i en Ampère (A)

Pour Accéder au QCM 1

II Le dipôle RL

Un dipôle Rl correspond à l’association série d’une bobine d’inductance L et de résistance interne r, avec une résistance R.

Lorsque le dipôle RL est soumis à t = 0 à un échelon de tension, l’équation différentielle vérifiée par le courant i (défini ci-contre) qui le traverse est :

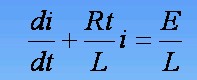
avec Rt = R + r

La solution de cette équation différentielle est, pour t > 0 ;

i(t) = E/Rt ( 1 – e^-(Rt/L).t)

Le quotient t = L/Rt, homogène à un temps, est la constante de temps du dipôle.

Pour déterminer expérimentalement sa valeur, on peut utiliser par exemple la courbe de i(t), dans le cas de l’établissement ou de la rupture du courant.

Pour accéder au QCM2

Simulation Excel sur circuit RL

JMPodvin Juillet 2002