Waves, Sound and Light
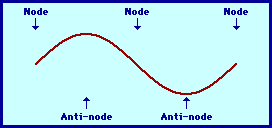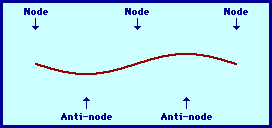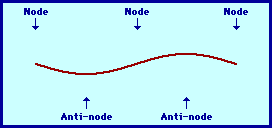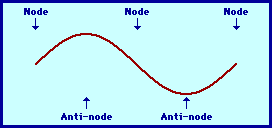
Second Harmonic
A standing wave pattern is a pattern which results from the
interference of two or more waves along the same medium. All standing
wave patterns are characterized by positions along the medium which
are standing still. Such positions are referred to as nodal positions
or nodes. Nodes are the result of the meeting of a crest with
a trough; this form of interference is known as destructive
interference and leads to a point of "no displacement." A node
is a point of no displacement. Standing wave patterns
are also characterized by antinodal positions - positions along the
medium that undergo maximum displacement from a high upward
displacement to a high downward displacement. Antinodes are
the result of a crest meeting a crest to form a supercrest and
a trough meeting a trough to form a supertrough. Standing wave
patterns are always characterized by an alternating pattern of nodes
and antinodes.
There are a variety of patterns which could be produced by
vibrations within a string, slinky, or rope. Each pattern corresponds
to vibrations which occur at a particular frequency and is known as a
harmonic. The lowest possible frequency at which a string
could vibrate to form a standing wave pattern is known as the
fundamental frequency or the first harmonic. The second lowst
frequency at which a string could vibrate is known as the second
harmonic; the third lowst frequency is known as the third harmonic;
and so on. An animation of a string vibrating with the second
harmonic is shown below.
The frequency associated with each harmonic is dependent upon the
speed at which waves move through the medium and the wavelength of
the medium. The speed at which waves move through a medium is
dependent upon the properties of the medium (tension of the string,
thickness of the string, material composition of the string, etc.).
The wavelength of the harmonic is dependent upon the length of the
string and the harmonic number (first, second, third, etc.).
Variations in either the properties of the medium or the length of
the medium will result in variations in the frequency at which the
string will vibrate.
For more information on physical descriptions of waves, visit
The Physics Classroom Tutorial.
Specific information is available on the following topics:
|