I. Rôle et caractéristiques d'un filtre
1. A quoi sert un filtre
2. Facteur d'atténuation
3. Gain en dB
4. Courbe de réponse
5. Bande passante- Fréquences de coupure
a. Filtre idéal
b. Filtre réel
II. Filtres électriques
1. Filtres RC
a. Filtre passe-bas
b. Filtre passe-haut
2. Filtres RLC
a. Filtre passe-bande
b. Filtre coupe-bande
3. Application : circuit d'accord (réception des ondes hertziennes)
-
Facteur d'atténuation
: Si E est l'amplitude du signal initial et S celle du signal de sortie
l'effet du filtre peut se mesurer par la grandeur

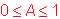 (facteur
d'atténuation, ou gain, dépendant de la fréquence
f). Plus A est proche de 0, plus la fréquence est atténuée.
(facteur
d'atténuation, ou gain, dépendant de la fréquence
f). Plus A est proche de 0, plus la fréquence est atténuée. - On peut également exprimer cette atténuation en décibels (dB) :
- Courbe de réponse en fréquence : c'est la courbe montrant les variations de A (ou de G) en fonction de la fréquence ;
- Bande passante. Fréquence de coupure
- si f1 et f2 ont une valeur finie, comme sur la figure, on a un filtre passe-bande.
- si f1=0 , f2 ayant une valeur finie,on a un filtre passe-haut
-
si f1 a une valeur finie avec
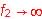 on a un filtre passe-bas
on a un filtre passe-bas - Filtres électriques
- Filtres RC
- en basse fréquence l'impédance du condensateur (rapport U/I ) est forte. A la limite, en courant continu, il est analogue à un interrupteur ouvert
- en haute fréquence son impédance est faible, elle tend vers 0 pour les très hautes fréquences : il est alors pratiquement analogue à un conducteur parfait.
- Filtres RLC passe-bande et coupe-bande
En optique, on peut utiliser par exemple un filtre rouge pour obtenir
à partir d'une lumière blanche polychromatique une lumière
rouge, par élimination des composantes bleue, verte, jaune... de
la lumière blanche. .
De manière générale,
le rôle d'un filtre est de supprimer ou d'atténuer fortement
le signal pour certaines fréquences, et de le transmettre presque
intégralement pour d'autres.
Appliqué à un signal complexe, un filtre est ainsi capable
de 'trier' les composantes du signal en fonction de leur longueur d'onde.
Pour chaque fréquence, on peut ainsi définir le facteur
d'atténuation dû au filtre :

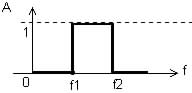 |
| Sa courbe de réponse serait de la forme ci-dessus, l'intervalle ]f1;f2[ étant appelé bande passante en fréquence du filtre. |
- f1 et f2 sont les fréquences
de coupure . Avec f1<f2:
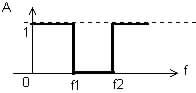 |
| On a un filtre coupe-bande si, f1 et f2 ayant une valeur finie, on a une courbe de réponse du type représenté ci-dessus |
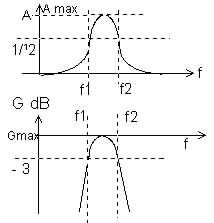 |
| La caractéristique d'un filtre réel est plus proche du
modèle représenté ci-dessus, avec Il est donc plus difficile de déterminer les limites de la bande passante. La convention généralement adoptée est celle de
la
bande passante à -3dB : on définit les fréquences
de coupure f1 et f2 comme les fréquences pour lesquelles G=-3dB
, ce qui équivaut à |
| Les différents circuits présentés sont étudiés
comme des filtres en tension
Le signal d'entrée ue et le signal de sortie us sont des tensions |
Ils utilisent les propriétés des condensateurs :
- Attention
toutefois
: le condensateur induit un déphasage , ce qui n'est pas le cas
pour l'interrupteur ou le conducteur parfait !
Comment fixer la frontière
entre haute et basse fréquence (courte ou longue période)
?
F
Le condensateur est toujours utilisé en association avec une résistance
.
La constante de temps RC sert
de durée de référence
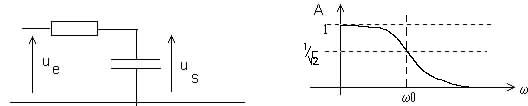 |
| On montre que la fréquence f0 de coupure à
-3dB est égale à |
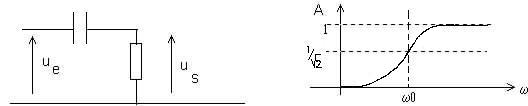 |
| On montre que la fréquence f0 de coupure à
-3dB est égale à |
On utilise les circuits oscillants LC , de fréquence propre
 |
| Pour une valeur donnée de la tension efficace
Ue, l'intensité efficace (ainsi par conséquent que la tension
efficace Us aux bornes de R) sont maximales pour la fréquence La largeur de la bande passante à -3dB est égale à La sélectivité du filtre est mesurée par
le facteur de qualité |
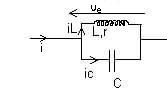 |
| Si une bobine non résistive (r=0) est en parallèle
avec un condensateur les intensités iL
et iC sont
en opposition de phase. On a donc D'autre part, pour la fréquence Les intensités dans les deux branches sont égales et en opposition de phase => leur somme est nulle On aura donc i=0 dans le reste du circuit : on parle de circuit 'bouchon' |
| En pratique r n'est jamais nulle .
Pour une bobine réelle de résistance r non nulle le comportement du circuit est similaire si r<<Lw0 . A la résonance l'intensité i n'est pas nulle , mais minimale. On a un filtre coupe-bande en intensité . La largeur de bande à -3dB et le facteur de qualité Q ont la même expression que pour le filtre série passe-bande. |
Pour un tel filtre , à la résonance, on a de fortes
surintensités dans chacune des branches. L'oscillateur
LC excité à sa fréquence de résonance oscille
'en circuit fermé' avec une grande amplitude au détriment
du reste du circuit.
Les ondes hertziennes engendrent dans les conducteurs de faibles courants alternatifs . En reliant un conducteur (antenne) à un circuit bouchon, on peut obtenir aux bornes de celui-ci une tension u non négligeable lorsque les fréquences des ondes hertziennes sont voisines de f0.
|
Exemple ci-contre : C=1nF, r=2W et L=10µH. L'intensité du courant i est égale à 1µA. Les courbes ci-contre représentent les variations de Ic et Ib (en haut) et Ue (en bas) en fonction de la fréquence. |
A partir d'une multiplicité de fréquences d'ondes hertziennes correspondant à tous les émetteurs existant, l'ensemble (antenne+circuit) permet de sélectionner celles voisines de f0.
Le circuit ne doit donc pas être trop sélectif.
Il doit toutefois l'être assez pour que les fréquences des radio de porteuse voisine soient suffisamment atténuées.
 |