Travail et énergie

Synthèse N° 14

I Travail d’une force

I.1 Travail élémentaire

Le travail d’une force quelconque au cours d’un déplacement élémentaire est W =

I-2 : Travail pour aller de A vers B

Le travail d’une force, lorsque son point d’application passe de A à B en suivant un chemin donné, est la somme des travaux élémentaires. Si ce travail ne dépend que de ces deux points et pas du chemin suivi, la force est dite conservative.

Le poids est une force conservative, son travail ne dépend que de z_A et de z_B

W(P) = mg(Z_A – Z_B)

I-3 Travail de la force extérieure appliquée à un ressort :

F = k.x (sens opposé à la force de rappel)

Le travail élémentaire donne dW = k.x.dx

Par intégration pour un allongement de x, le travail effectué par la force qui tire sur le ressort est donné par

W = ½ kx²

II Energie potentielle

II-1 Energie potentielle de pesanteur d’un solide de masse m

Cette énergie est donnée par

E_pp = m.g.z (ou z est l’altitude du centre d’inertie de l’objet dans le référentiel d’étude, l’axe des z est orienté vers le haut)

II-2 Energie potentielle élastique d’un ressort

L’énergie potentielle de la force de rappel est égale à E_pk = ½ kx²

III Energie mécanique

III-1 Energie mécanique d’un système solide –ressort horizontal

Cette énergie dans un référentiel donné, est la somme de son énergie cinétique et de l’énergie potentielle élastique du ressort. Lorsque l’origine O du repère est confondue avec la position du centre d’inertie G au repos, elle s’écrit

E_m = E_c + E_pk = E_c + ½ kx²

Accéder à l’applet de Walter Fendt (observer les variations d’énergie potentielle et d’énergie cinétique)

III-2 Energie mécanique d’un solide dans le champ de pesanteur

Elle est égale à la somme de l’énergie cinétique et de l’énergie potentielle de pesanteur :

E_m = E_c + E_pp = ½ mv² + mgz

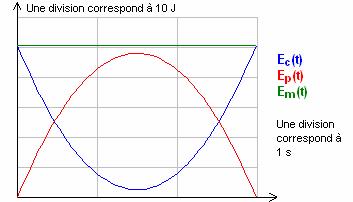
Ci-dessus les variations d’énergie d’un ballon lancé en l’air

Em est conservée

Accéder à l’applet de Walter Fendt sur le pendule (observer les variations d’énergie potentielle et d’énergie cinétique)

III-3 Conservation et non conservation de Em

L’énergie mécanique se conserve si :

Le travail des forces autre que F_rappel est nul, pour un système solide- ressort

Le travail des forces autres que P (poids) est nul, pour un solide dans le champ de pesanteur

JMPODVIN - 2003