Systèmes oscillants
Synthèse N° 12
I Le pendule
simple
I-1 Définition
Un pendule simple est
constitué par un solide de petites dimensions, suspendu à un fil de longueur l
dont la masse est négligeable devant cette du solide.
I-2 Position d’équilibre
stable du pendule simple
La position d’équilibre d’un
oscillateur est sa position naturelle lorsqu’il est immobile dans le
référentiel d’étude, et soumis uniquement à son poids et à la réaction du
support.
Pour un pendule simple cette
position est la position verticale en dessous de l’axe de rotation (on verra
que dans ce cas son énergie potentielle est minimale)
I-3 Position d’un
pendule ou d’un oscillateur
L’écart à l’équilibre d’un
pendule est repéré par un angle θ
(abscisse angulaire)
L’amplitude angulaire des
oscillations non amorties est la valeur absolues θ0 des
valeurs extrêmes de θ.
La période du pendule est la
durée d’un aller et d’un retour entre 2 positions identiques du pendule, quand
les oscillations sont amorties, on parle alors de pseudo période.
Comparer la variation de
la période et de la pseudo-période quand l’amortissement varie en utilisant
l’applet de JJ Rousseau ci-dessous
I-4 Isochronisme des
petites oscillations
Deux pendules de même
longueur placés en un même lieu, auront la même période si leur amplitude
angulaire est inférieure ou égale à 10°
I-5 Période propre
La période propre T0
d ‘un pendule simple de longueur l dont
l’amplitude angulaire est faible est donnée par
T0 =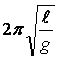 
g = valeur de la pesanteur
Faire varier la longueur du
pendule et vérifier que la période est bien celle indiquée ci-dessus ® Applet de Walter Fendt
II Oscillations forcées
d’un pendule simple
Un pendule (ou résonateur)
est mis en oscillations forcées lorsqu’il est soumis à l’action d’un excitateur
qui lui impose une période d’oscillation.
Quand la période de
l’excitateur est voisine de la période propre du résonateur, on observe un
phénomène de résonance.
JM Podvin Juillet 2002
