Satellites et
planètes
Synthèse P 10
I Mouvement
parabolique
Dans le champ de pesanteur,
quand les actions de l’air sont négligées, la seule force qui agit sur un
projectile en mouvement est son poids.
On peut alors en déduire l’expression
de a, v, et les équations horaires paramétriques du centre d’inertie du
projectile
Dans le repère 
, le vecteur accélération de G a pour coordonnées
·
ax
= 0 et az = -g
Par intégration des
coordonnées de 
, on obtient les coordonnée du vecteur vitesse de G dans le
repère 
:
·
Vx
= V0x et VZ = -gt + VOZ
Une nouvelle intégration
donne les équations horaires paramètriques de G :
·
x =
VOX.t et z = - ½ gt²+ VOZ.t
( G est en O à la date t = 0)
Ci-contre la trajectoire d’une boule de pétanque lancée
avec une vitesse initiale de 15 m/s et un angle α
= 77° Les vecteurs bleus sont les vecteurs vitesse Les vecteurs verts les vecteurs accélération
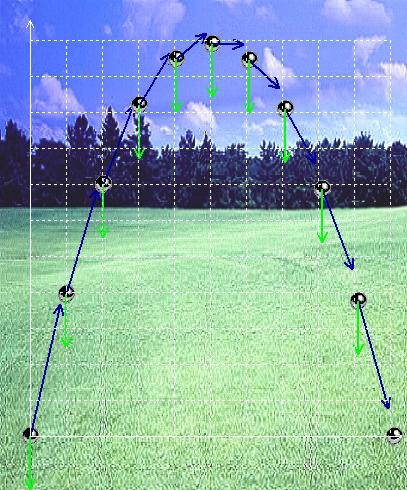
Dans les 2 animations qui suivent, on s’aperçoit que
la vitesse horizontale reste la même tandis que la vitesse verticale varie, la
trajectoire des projectiles est une parabole
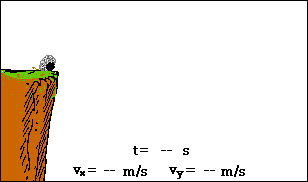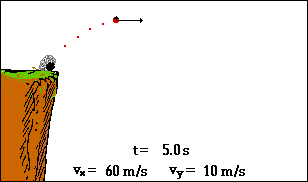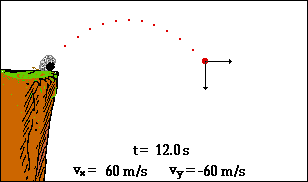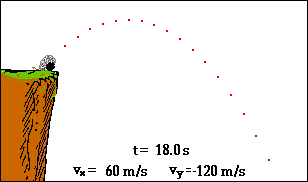
La balle retombe dans le camion qui roule à vitesse
constante
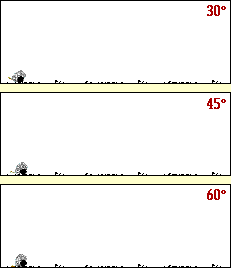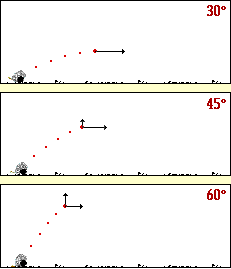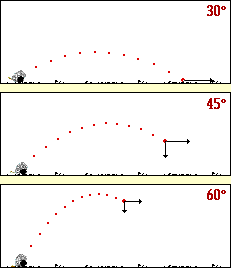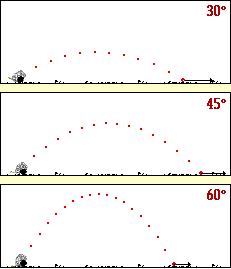
L’animation ci-dessous vous donne l’évolution de la
portée du tir en fonction de l’angle de départ
On pourra aussi remarquer la hauteur max atteinte dans
les trois cas
La valeur de la vitesse initiale est la même .
II Mouvements
des planètes et des satellites
II-1 Les 3 lois de
Kepler appliquées aux planètes
Première loi : dans le référentiel héliocentrique, les
centres P des planètes décrivent des orbites elliptiques ayant le centre S du
Soleil pour foyer ; simulation cliquer ici
Deuxième loi : le rayon vecteur SP balaie des aires constantes
pendant une durée donnée. Simulation cliquer ici
Troisième loi :
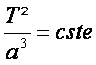
ou T est la période de
révolution et a la longueur du demi -grand axe de l’ellipse.
II-2 Loi de gravitation
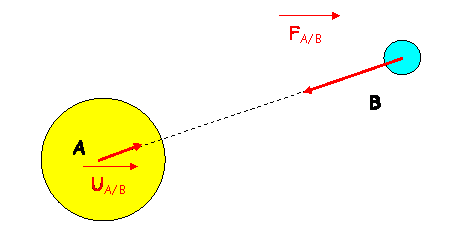
La force gravitationnelle 
de A sur B a pour expression
où G = 6,67.10-11
m3.kg-1s-2 est la constante de gravitation
universelle.
A et B ont leur masse à
symétrie sphérique.
II-3 Mouvement
circulaire uniforme du centre d’inertie
Lorsque le centre d’inertie G
d’un objet est en mouvement circulaire uniforme de rayon r et de centre
O , la valeur v de sa vitesse est constante. Le vecteur vitesse n’est pas
constant car sa direction varie
v = w. r ( ou w est la vitesse angulaire de G)
Son vecteur accélération est
centripète et a pour valeur:
a = v²/r = rw²
L’application de la deuxième
loi de Newton pour le mouvement circulaire d’un objet autour du Soleil ou
autour d’une planète donne :
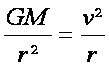soit 
M étant la masse du Soleil
pour le mouvement des planètes, ou de la planète pour le mouvement des
satellites.
II-4 Satellites
géostationnaire
Dans un référentiel
géocentrique, un satellite géostationnaire est en orbite circulaire dans le
plan équatorial. Sa période de révolution est de 24 h environ, et le rayon de
la trajectoire proche de 42.103 km
