Mouvements de
chutes verticales
Synthèse P10
I Force de pesanteur et champ de pesanteur
I-1 La force de
pesanteur
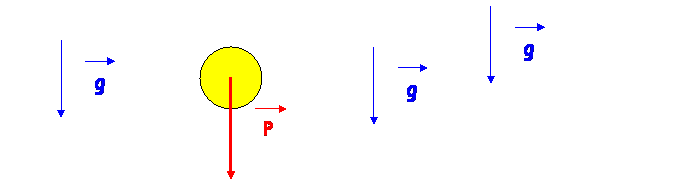
La force de pesanteur 
exercée sur un objet de masse m, dont le centre d’inertie est
placé au voisinage de la Terre est donnée par :
La force de pesanteur a même
sens et même direction que le vecteur 
(champ de pesanteur)
I-2 Le champ de
pesanteur
Il varie avec l’altitude et
la latitude du point où se trouve l’objet.
On le considérera
comme localement uniforme pour tous les mouvements de petite portée
Dans ce cas :
Sa direction est verticale
Son sens est vers le bas
Sa valeur (à Paris au niveau
du sol est de 9,81 N.kg-1)
II Force
agissant sur un solide tombant dans un fluide
Un solide tombant dans un
fluide est soumis à :
-
la
force de pesanteur
-
la
poussée d’Archimède
-
la
force de frottement fluide
Les forces de frottement
fluide dépendent de la vitesse et de la forme du solide en mouvement dans le
fluide. Elles sont toujours de sens opposé au mouvement.
Parmi des différentes
possibilités, il existe deux types de forces de frottement fluide f
-
aux
très faibles vitesses f = k.v
-
aux
vitesses moyennes f = kv²
III Chute verticale avec frottement
Soit v la composante de la
vitesse du centre d’inertie du solide sur un axe vertical descendant. Lors
d’une chute verticale dans un fluide immobile, l’équation différentielle de
v(t) s’écrit :
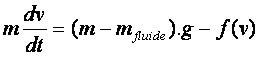
ou f(v) est la force de
frottement du fluide sur le solide considéré.
Si le mouvement dure assez
longtemps, la vitesse tend vers une valeur asymptotique vlim appelée
vitesse limite, qui vérifie la relation :
(m – mfluide).g = f(vlim)
On peut grâce à cette
relation et avec la méthode d’Euler obtenir une solution approchée de
l’équation différentielle et vérifier la forme de la force de frottement (kv,
kv², autre forme)
Tester une chute avec
frottements ( on pourra faire varier le rayon de la balle et vérifier
l’influence sur la vitesse limite)
IV Chute verticale libre
Axe des z dirigé vers le
haut :
Dans ce cas la seule force agissant
sur le solide est la force de pesanteur.
L’accélération du centre
d’inertie est égale au vecteur champ de pesanteur g (ou accélération de la
pesanteur)
ou k est le vecteur
unitaire suivant l’axe z dirigé vers le haut
On déduit la vitesse en
intégrant a et en tenant compte de la vitesse initiale du solide
v(t) = -gt + v0
Puis on déduit l’altitude z
en intégrant v(t) par rapport à t.
z(t) = - ½ gt² + v0t
+ z0
Le mouvement est un mouvement
uniformément accéléré.( accélération constante –g)
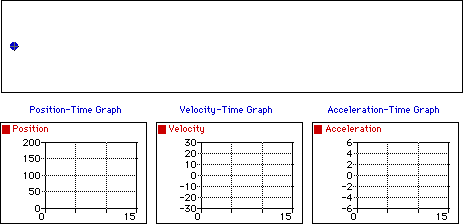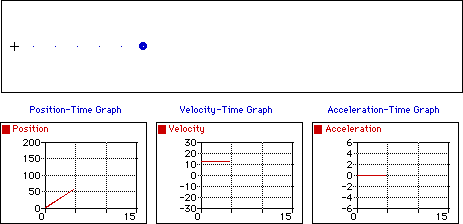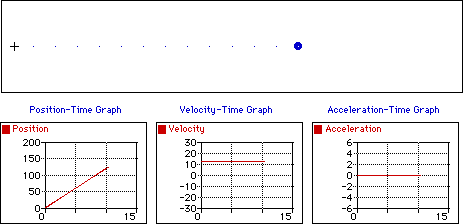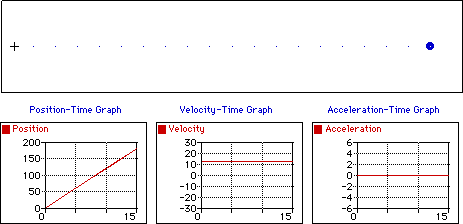
Ci dessous on donne les
caractéristiques de deux types de mouvements.
Un mouvement rectiligne et uniforme
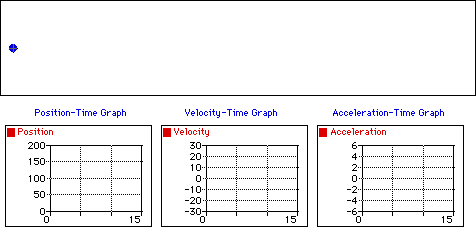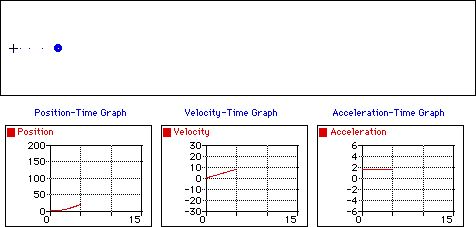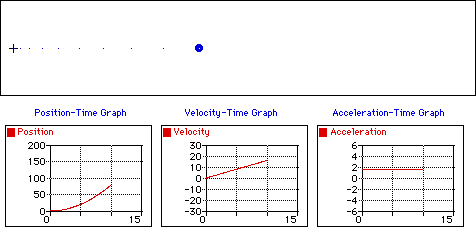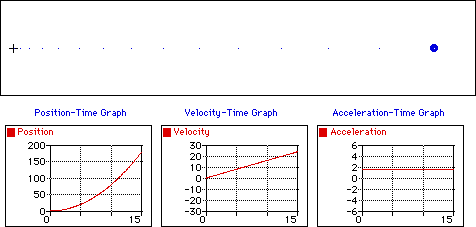
Un mouvement rectiligne uniformément
accéléré
JMPodvin Juillet 2002
