Le pendule élastique
Synthèse P13
(Applet JF Garcia)
I Force de
rappel
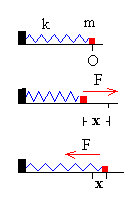
La force de rappel d’un ressort
de constante de raideur k et qui s’est allongé de x (m) est donnée par F = -kx
(F en N, x en m, k en N/m)
Exercice
A l’aide de l’applet
ci-dessous, calculer la constante de raideur du ressort
Pour cela ajouter une à une des
masselottes de 50 g à l’extrémité du ressort, des valeurs s’inscrivent alors
dans la colonne de gauche, quand vous avez six ou sept valeurs, cliquer sur
grafica, pour que l’applet trace F e n fonction de x.
Déduire alors la constante de
raideur
Cliquer sur nuevo, pour
recommencer l’expérience avec un autre ressort.
|
|
II Mouvement
horizontal d’un solide soumis à l’action d’un ressort
Les
forces qui agissent sur ce type de mobile sont son poids, la réaction normale
du support, et la force de rappel du ressort
Suivant
l’axe horizontal seul la force de rappel possède une composante, on en tire en
appliquant la seconde loi de Newton que
-k.x
= m.ax ® on en tire que kx + m ![]() =0
=0
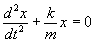
La
solution de cette équation différentielle est : x = 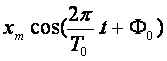
xm
est l’amplitude du mouvement, et ![]() est la phase à l’origine des dates.
est la phase à l’origine des dates.
La
période propre des oscillations est donnée par

Pour
un amortissement faible, le mobile oscille avec une pseudo période proche de sa
période propre.
Lorsque
l’oscillateur est fortement amorti, le mouvement est apériodique.
Exercice
Avec l’applet
ci-dessous vous pouvez, mesurer la période d’oscillation du pendule ( nuevo
accrocher une masse, puis cliquer sur empieza, déclencher le chronomètre
mesurer 10 oscillations)
On peut alors
déduire la valeur de T0 puis déduire k.
Sans appuyer sur nuevo
, ajouter un seconde masse et réitérer l’expérience ( comparer la valeur de k
avec la précédente) etc….
|
|
III
Oscillations forcées
Un
oscillateur soumis à l’action d’un autre oscillateur lui imposant sa période
d’oscillation est mis en oscillations forcées ; l’oscillateur qui impose
la période est appelé excitateur ; l’oscillateur excité est appelé
résonateur.
Pour
une période caractéristique du résonateur, l’amplitude des oscillations forcées
est maximale : il y a résonance.
Pour
visualiser le phénomène utiliser l’applet de Walter Fendt
JM PODVIN 2005