CORRECTION : Circuit RC

QUITTER

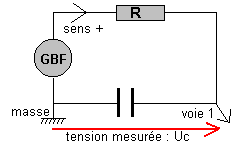
1°) a)
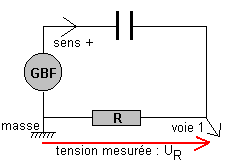
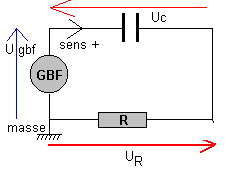
remarque : Une fois le sens + indiqué ( sens du courant délivré par le GBF réglé en tension carrée) la flèche de tension représentant Uc doit être en sens inverse du sens de courant de charge (sens +). Si on inverse la masse et la voie 1 on mesurera -Uc.

 q1.gif (1345 octets)

1°) b)
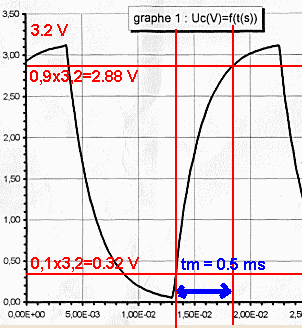
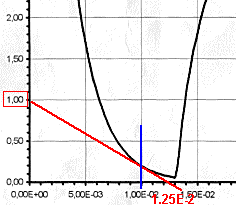
Temps de montée : tm = 0.5 ms = 5.10-3 s
(voir détermination graphique)
Constante de temps :
t = tm/2,2 = 5.10-3 /2,2     t= 2.27.10-3 s

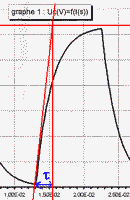
autre méthode : La tangente au début de la charge coupe Umax à la date t
(schéma ci-contre non demandé dans la question)		 q11.gif (2860 octets)
q2.gif (14815 octets)
1°)c      t dépend de R et C: R ( W) C (F) et t (s)

Analyse dimensionnelle
U = R.I Þ R =U/I  ( V/A)
Q = C.U   Þ    C = Q/U = I.t/U ( A.s/V)		 Þ R..C (V.A.s/V.A) donc t = R.C
 

Calcul de C  : t = R.C      C = t / R  = 2,27.10-3/2082 = 1,1.10-6 F  = 1100.10-9 F    C = 1100 nF
2°)a     On visualise UR : tension aux bornes du conducteur ohmique. UR(t) = R.i(t). Les variations de UR en fonction du temps représentent les variations de i au cours du temps à la constante R près.

Remarque : Il a fallu déplacer le conducteur ohmique pour que la masse de l'oscillographe corresponde à celle du GBF

q2a.gif (1375 octets)
2°)b     Le graphe 3 représente i= f(t)
Justification :  Pendant la charge du condensateur i doit être positif (sens +) et donc i doit être négatif pendant la décharge

Remarque : le schéma ci-contre montre une superposition de U=f(t)(en rouge)  avec i = f(t) ( en noir)

 

q2b.gif (5925 octets)

2°)c     
A tout instant  : loi d'addition des tensions :
Ugbf(t) = Uc(t)+UR(t)
-Au début de la charge  : Uc = 0 V
Ugbf = 0 + R.i0   Þ i0 = Ugbf / R = 3.2/2082 = 1.54.10-3A
i0 =1.54.m A
-A la fin de la charge : Uc = 3.2 V et donc UR = 0 V
UR = 0 Þ i0 = 0 A

q2c.gif (1477 octets)

-A une date quelconque : t = 10 ms
A tout instant t : i = dq/dt  et q = C.Uc donc i = C.dUc/dt
Graphiquement dUc/dt représente le coefficient directeur de la tagente à Uc() au temps  = 10 ms (voir graphe ci-contre) .
mesure:  dUc/dt = 1 / -1,25.10-2
i =  C. dUc/dt = 1,1.10-6.(-1/1,25.10-6) = -8,8.10-5 A
i = -88 µA  ( pendant la décharge i est négatif, voir question 2b)

 

 q2c2.gif (6847 octets)

3°)a     
1er cas R = 9800 W ; C = 0,1.10-6 F
RC = 9,8.10-4 s
2ème cas : R = 4975 W ; C = 2 .10-6 F
RC = 99,5.10-4 s.
Graphe 4 : temps de charge le plus court donc cas n°1
Graphe 5: temps de charge le + long donc cas n°2

q3a.gif (4752 octets)

3°)b  
Oscillations de relaxation : Le système évolue entre 2 états extrèmes, le passage de l'un à l'autre se fait périodiquement.
Première partie : le condensateur stocke de l'énergie
Deuxième partie : il restitue de l'énergie
Analogie mécanique : le VASE DE TANTALE

Description du fonctionnement du vase de tantale
( non demandé dans la question )
Un robinet d'eau alimente à débit constant un vase muni d'un siphon. Quand l'eau ateint le niveau h1, le siphon s'amorce et le vase se vide jusqu'au niveau h0. Le remplissage reprend alors. Le phénomène est analogue au fonctionnemen du condensateur.

 q3b.gif (2346 octets)

JF Noblet  htp://perso.infonie.fr/jf_noblet/index.htm

QUITTER